Mapa de karnaugh
Se denomina así en honor a George Boole.
En la actualidad, el álgebra de Boole se aplica de forma generalizada en el ámbito del diseño electrónico. Claude Shannon fue el primero en aplicarla en el diseño de circuitos de conmutación eléctrica biestables, en 1948. Esta lógica se puede aplicar a dos campos:
- Al análisis, porque es una forma concreta de describir como funcionan los circuitos.
- Al diseño, ya que teniendo una función aplicamos dicha álgebra, para poder desarrollar una implementación de la función

Mapa de Karnaugh
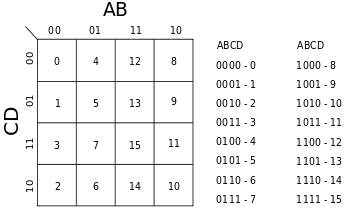
Las variables de entrada pueden combinarse de 16 formas diferentes, por lo que el mapa de Karnaugh tendrá 16 celdas, distribuidas en una cuadricula de 4 × 4.
La combinación de dígitos binarios en el mapa representa el resultado de la función por cada combinación de entradas. Por ejemplo, la celda en la esquina superior izquierda del mapa es 0, porque el resultado de la función es ƒ = 0 cuando A = 0, B = 0, C = 0, D = 0. De igual manera, la esquina inferior derecha es 10 porque el resultado de la función es ƒ = 10 cuando A = 1, B = 0, C = 1, D = 0.
Una vez construido el mapa de Karnaugh, la siguiente tarea es la de seleccionar conjunto de terminos denominados subcubos de manera que se obtenga el menor número de subcubos posible.Estos subcubos se seleccionan formando grupos de rectángulos que encierren a los unos del mapa, las áreas deben ser potencia de 2 (ej. 1, 2, 4, 8, ...) y se debe tratar de agrupar el mayor número de unos posible. En resumen hay que tomar en cuenta al hacer estos grupos de unos (subcubos) lo siguiente:
- Debemos utilizar todos los unos del mapa.
- Es mejor crear el menor numero de grupos.
- Los unos pueden estar en varios grupos.
- El número de unos dentro de un grupo debe de ser cualquier potencia de 2.
- Mientras más grande sea un grupo la simplificación de la función será mejor.
- No es necesario que todos los grupos tengan el mismo tamaño.
Qué términos seleccionar va dependiendo de cómo se quiera realizar la simplificación, puesto que esta puede realizarse por minitérminos o por maxitérminos.
4.5.2 Mapas de Karnaugh. Las formas normales disyuntivas y conjuntivas son útiles para varios propósitos, tales como determinar si dos expresiones representan la misma función booleana. Para otros propósitos son a menudo engorrosas por tener mas operaciones de las necesarias. Un método para lograr definir una expresión más simple que otra es el método de los mapas de karnaugh que simplemente son diagramas de Venn con las distintas regiones arregladas en cuadros dentro de un rectángulo.
Para funciones de más de cinco variables, este método se vuelve muy complicado y pierde utilidad.
A continuación se verán las diferentes clases de mapas de Karnaugh.
Mapa de una variable,

Mapa de dos variables

Mapa de tres variables

Mapa de cuatro variables